If you ask maths teachers what they would like to teach students that isn’t currently assessed or mandated (and we have!), they will often say something like ‘topology’, ‘Mobius strips’ or ‘fractals’.
It is an interesting omission from the current English mathematics curriculum that we aren’t really exploring ideas about fractals – recursive shapes like Romanesco broccoli, ferns and coastlines – with young children. Why? Ideas about iteration and recursivity come up when we look at sequences at higher KS4 and KS5, but often this is the first time students consider them – in mathematics, anyway.
In art, infinity mirrors are a simple way to create a startlingly effective image. Yayoi Kusama is one artist who has used them, such as in this Hirshhorn exhibition. Here is our colleague Ellen standing inside one of these extraordinary pieces:
Recently, a beautiful Reddit thread once again brought mathematics and art together in the form of recursivity. A user posted a picture of their mother holding a painting of a crane (the bird not the machine).
Source: Reddit
Another user painted a picture of the mother holding a painting of a crane…and a chain of mathematical and artistic fun was born.
Source: Reddit
Source: Reddit
To make matters more interesting, the chains also split at certain points, too, such that someone had the helpful idea of drawing a tree diagram to keep track:
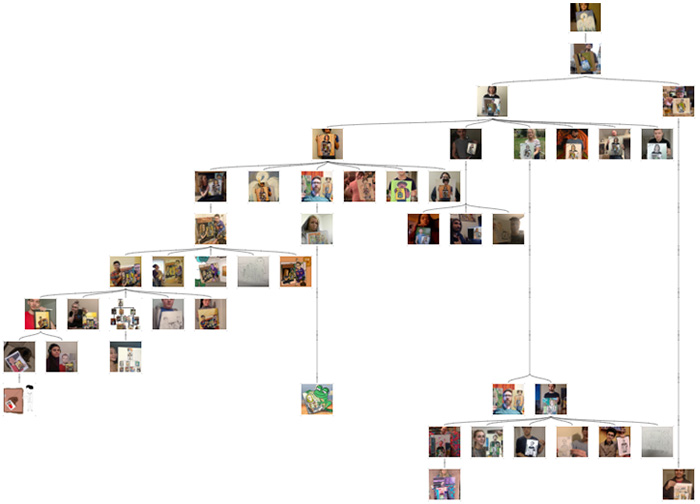
Source: GitHub
We could ask the much broader question here: to what extent is art linked to maths? To what extent can one support the other?
Hickman and Huckstep (2003) suggest that the purposes of art and maths are similar, and therefore there is reason to believe that improving understanding of one will improve understanding of the other. Yet often art is associated with expression, feelings and affect, whereas maths is seen as the opposite – lacking expression and affect. Fortunately, one writer, Morris Kline, has challenged this and suggested that maths has an emotional facet and thus has more in common with art than some may think (Hickman and Huckstep, 2003). As artists and art admirers experience the feelings of joy, surprise and enjoyment when exploring creative pieces, mathematicians often experience similar positive feelings through their work. Whether such feelings are a result of solving a mathematical problem or seeing a student grasp a concept they have been struggling with, the feeling of happiness, satisfaction and accomplishment is no doubt the same as the feeling of happiness, satisfaction and accomplishment experienced by an artist who completes a painting after six months or when they hear praise during their first exhibition. However, this is only one example of how maths and art are similar. According to Dienes (2004, cited in Mann, 2006), both mathematicians and artists communicate with others through their work. They both play with ideas and combine them in different ways until they are happy with the final product.
But even if maths and art have emotion in common, does this mean anything for the curriculum or the classroom? Edens and Potter (2007) suggest that art appears perfectly suited to teaching visual and spatial skills, which can be beneficial in mathematics. The researchers argue that with greater emphasis on cross-curricular links, there is a need for research to examine the value of art and the transfer of art to other subject (Edens & Potter, 2001 as cited in Edens & Potter, 2007). Edens and Potter (2007) conducted a study investigating the relationship between students’ spatial understanding and mathematical problem solving. Students aged nine to eleven were given tasks that measured their level of spatial understanding, problem solving and whether their drawings were schematic or non-schematic. Children’s drawings were rated as schematic if they met certain criteria assessing proportional thinking and evidence of using the drawing to solve maths problems (see Figure 1 for an example of schematic and non-schematic drawings).
A new pupil comes into our class who is 40cm shorter than the teacher and 11cm taller than you. You are 130cm and the teacher is 173cm. Show how you can draw a picture to work out how tall the new pupil is.
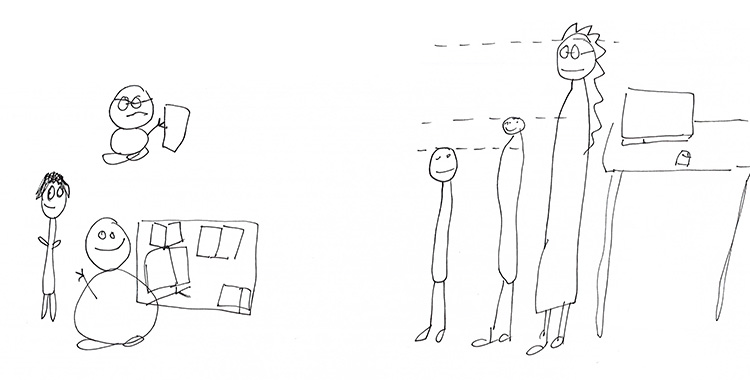
Figure 1. An example of a non-schematic drawing (left) and a schematic drawing (right). Note that elements may be present in both schematic and non-schematic drawings that are not relevant to the problem (books, desk, environmental features, facial expressions) but the key difference is schematic drawings show the representation of a proportional relationship, or some sense of one.
The study found that students’ levels of spatial understanding were positively correlated with problem solving and that students with the highest levels of spatial understanding were more successful at problem solving than those with the lowest levels of spatial understanding. Furthermore, students producing high-level schematic representations tended to score higher on problem solving tasks.
Earlier research has also demonstrated a link between spatial representations and mathematical problem solving. Hegarty and Kozhevnikov (1999) investigated how spatial and visual imagery affected problem solving in mathematics. They also assessed children’s use of schematic and non-schematic (pictorial) representations and found that the use of schematic representations was positively correlated with mathematical problem solving. They concluded that schematic spatial representation includes the spatial relationships relevant to solving problems in maths. Bronsan and Fitzsimmons (2001, cited in Mann, 2006) suggest that if students do not have the opportunity to approach a problem creatively, their problem solving skills are limited to recalling methods created by others.
So maybe art and maths have more in common than originally thought. Maybe both elicit emotion? Maybe skills in one can improve understanding of the other? Edens and Potter (2007) suggest that teachers can use a child’s drawing to judge their level of spatial understanding and therefore could use this information to support students. They also suggest that the art room could create good contexts for developing students’ spatial understanding: skills associated with both artistic and mathematical abilities. As more inter-disciplinary research emerges across fields, perhaps this cross-curricular approach is worth exploring further?
References:
Edens, K. & Potter, E. (2007). The Relationship of Drawing and Mathematical Problem Solving: Draw for Math Tasks. Studies in Art Education, 48(3), 282–298. https://doi.org/10.1080/00393541.2007.11650106
Freiberger, M. (2007, March 1). Perfect buildings: the maths of modern architecture. Plus. Retrieved from https://plus.maths.org/content/perfect-buildings-maths-modern-architecture
Hegarty, M. & Kozhevnikov, M. (1999). Types of visual-spatial representations and mathematical problem solving. Journal of Educational Psychology, 91(4), 684–689. https://doi.org/10.1037/0022-0663.91.4.684
Hickman, R. & Huckstep, P. (2003). Art and Mathematics in Education. Journal of Aesthetic Education, 37(1), 1–12. https://doi.org/10.2307/3527417
Mann, E. L. (2006). Creativity: The essence of mathematics. Journal for the Education of the Gifted, 30(2), 236–260.
Join the conversation: You can tweet us @CambridgeMaths or comment below.