Intrigue and curiosity should be a part of everybody's learning. One way to engage with geometry is to consider Kanizsa figures., such as the one below (the Kanizsa triangle).

Kanizsa figures challenge your perceptions, because you see what's not actually there but what's insinuated by the clever use of lines, contours and sometimes colour.
Italian psychologist Geatano Kanizsa first described this optical illusion in 1955 as a subjective or illusory contour illusion. The study of such optical illusions has led to an understanding of how the brain and eyes perceive optical information and has been used considerably by artists and designers alike. They show the power of human imagination in filling in the gaps to make implied constructions in our own minds.
Kanizsa figures and similar illusions are a really useful way to encourage learners to 'say what they see' and to explain how they see it. It offers a chance for others to become aware of the different views available in a diagram and share their own thoughts without the 'danger' of being wrong; many people see different things.
Visual perception is an integral part of learning and 'seeing' is " not a passive activity but involves active construction on the part of the viewer"1. Learning to 'see' in geometry involves discerning features, breaking down and building up geometrical figures, and identifying relationships, as well as articulating these ideas to others and communicating clear and concise descriptions, arguments and conjectures.
What better way to do this than with an optical illusion?
However, the ability to discern information from an incomplete picture is also a useful geometrical tool. A good starter for a lesson on this might ask: what shape are Mickey Mouse's ears? (we only ever see 2D representations from many angles…the inference is that they are spherical, as all the views give circular profiles!)
We can also consider the rings of Saturn. Since we know that Saturn has rings we can infer their 3D shape from a 2D photograph:

But go back in time and various drawing of Saturn show that previous astronomers were not quite so accurate. Galileo showed how mathematical understanding could be put to use in a creative way. He was the first astronomer to observe Saturn's rings, at first thinking they were moons on either side of the planet, causing him to describe the planet as 'triple-bodied'. This was his first guess at an image of Saturn:

Imagine his astonishment when later he observed that the objects either side had disappeared - he wrote "I do not know what to say in a case so surprising, so unlooked for and so novel". He had, in fact, seen the rings edge-on from the Earth's perspective (called a ring plane crossing). Another, later, observation showed two half-ellipses. He now deduced something more like our own idea of Saturn today:

What to conclude? What shape could these mysterious objects be? Were they solid?
It took several more astronomers, keenly observing and recording, before the true shape of the rings of Saturn were clearly understood. Because of the huge distance we are from Saturn and the complexity of its makeup, we are still refining and reviewing our ideas of its shape. For example, until 1980 it was thought that Saturn had exactly seven rings - now we know there are potentially hundreds: ringlets within rings. With partial information about shapes, we must use our mathematical understanding to scientifically estimate the best guess we can make that fits the known facts - and this is liable to change as we get new information.
Similarly, Friedrich August Kekule dreamed that the benzene molecule was a hexagonal ring in 1850, a fact that was accepted but not actually seen until the 1980s.
So sharing optical illusions will benefit your pupils' confidence, ability to use their imagination, explain their ideas and possible even more! Do share any good ones that you have come across with us here at Cambridge Mathematics.
1. Johnston-Wilder, J. and Mason, J. Developing Thinking in Geometry (2005), Open University
|
SOMETHING TO TRY:
What can you see?
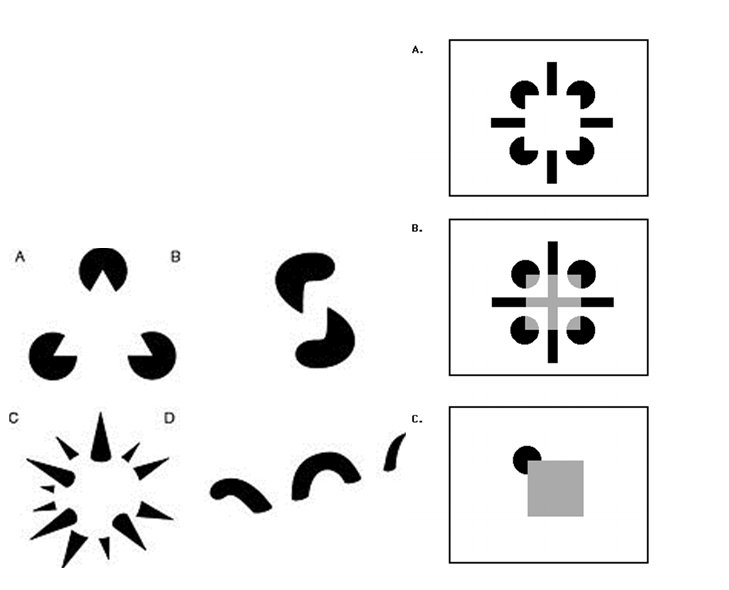
(images from here and here)
How many triangles can you find?
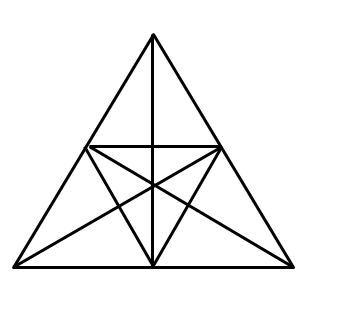
|