Recently, maths Twitter enjoyed explaining to the world at large why one large pizza was (usually) better than two small ones. Perhaps counterintuitively, the total area of an 18’’ large pizza is somewhat larger than two small 12’’ pizzas, as shown below:
Source: @Fermat’sLibrary
This taps into some of the weird ideas humans have around areas and circles. For example, the so-called dinner-plate problem similarly astounds people – asking what percentage increase in food one could fit on a plate that increases by 3 inches in diameter from 9” to 12” (this problem shares with the one shown above the issue that it is actually three-, not two-dimensional)1. It is also interesting to note that this mirrors social trends in the Western world in the last fifty years or so, with ‘dinner’ size plates generally increasing in size by approximately this amount, and that some research suggests larger plates encourage greater food consumption (although some find the opposite).
What would you estimate the answer to be?
Of course, the pizza problem is all wrong. ‘Small’ pizza sizes, on average, centre around the 9” diameter mark, and you’d be hard pushed to find an 18” diameter pizza (Papa John’s’ XXL one is only 15.5” across). Similarly, even maths graduate and communicator Eddie Woo’s explanation of this issue fell into the age-old trap of confusing radius and diameter, suggesting enormous 32”-diameter pizzas – which is approximately the size of an adult spacehopper (below is his redrawn diagram when he realised his mistake). We are pretty bad at thinking about circles, on the whole.
So what is the real picture when we look at pizza sizes? When looking at this issue, we suggest a few more dimensions are important than just size:
- choice (which flavour/s of pizza do I want?)
- coverage (does my chosen pizza provider service my area or deliver for free/a cost?)
- price (at which price points do I get the best deals?)
It is unlikely we could focus on all of these at once, so here is an attempt to consider the latter without worrying too much about the former (all pizzas used for this data are cheese and tomato):
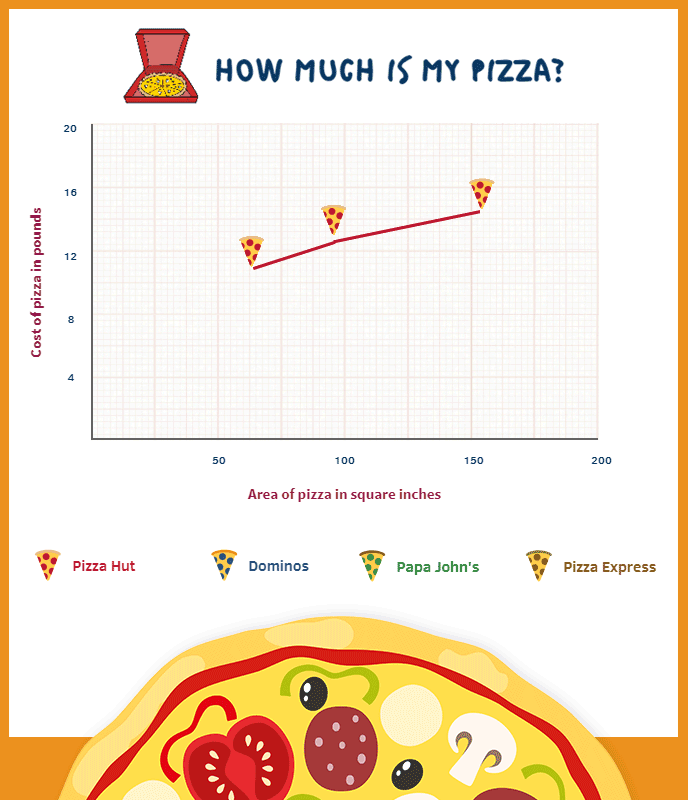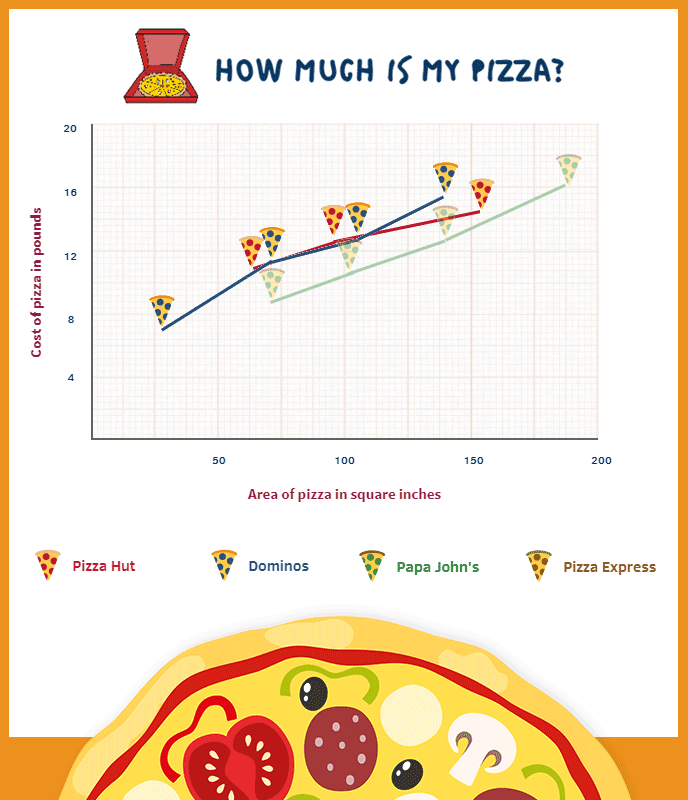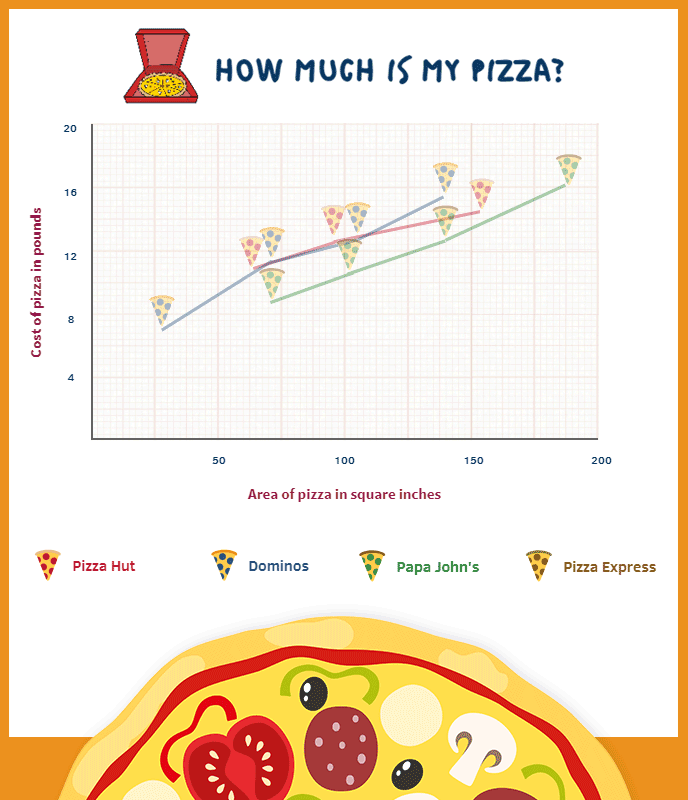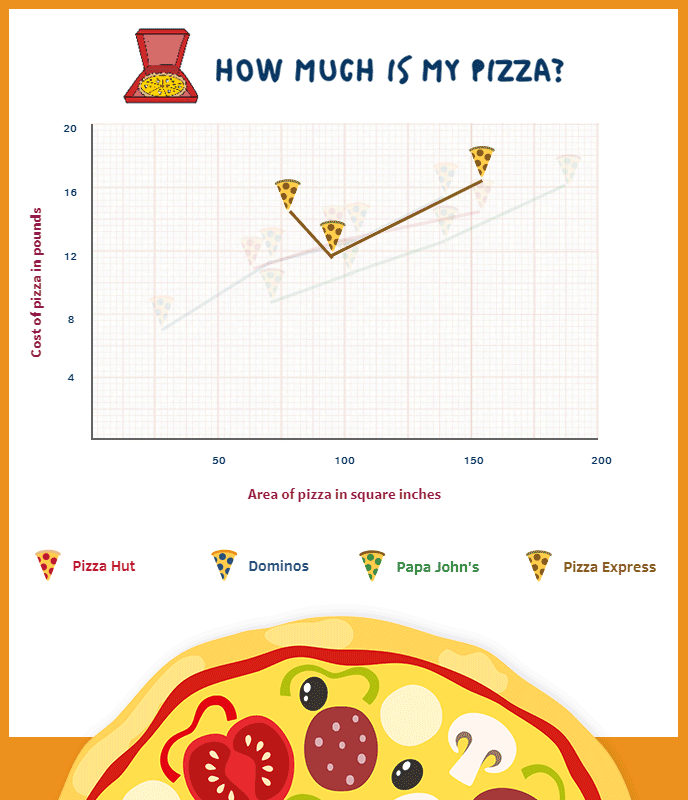
While the analysis between three (approximately standard) sizes of pizza is all well and good, we could further complicate this discussion due to a range of pizza created by Pizza Express known as the Leggera pizza. This collection can only (well…maybe not only) be described as the lovechild of a polo and a pair of ripped jeans. During the birth of this monstrosity, a large part of its torso is taken, the wound filled with salad instead of gauze, and to add insult to injury it is actually more expensively priced than a non-wounded sibling. You might think consumers would be furious at this mistreatment. However, it is marketed with a concomitant explanation about the reduction in calories – a concept that sounds dramatically more pleasing than ‘we gave you much less of what you really wanted, but please enjoy the rabbit food we’ve left in its grave’. It’s a marketing manager’s dream: consumers spending money to receive less – even more so if the removed centre is then sold on as a small pizza (we cannot find any evidence either for or against this conjecture so far). Notice the Pizza Espress line on the graph and how the Leggera presents a clear outlier (can you see which one it is?).
If we move past the possible overreaction to the shape of the Leggera we come to two interesting and related questions:
- What percentage of the pizza surface is removed in a standard 11” Leggera pizza (the hole measures approx 4.8” in diameter)? Try and estimate before you work it out.2
- What size Leggera pizza, keeping the hole in proportion, would be required to have the same surface area as a circular 11” pizza? Tweet us @CambridgeMaths or comment below with your worked solution.
References:
1The solution is around 78% if the food on the plate is considered in some sense ‘flat’
2approx 19.7%