Have you ever given blood? If you have, you may have a sense of how much blood you donated – if not, you can probably still make a good estimate of how much blood is taken during a blood donation session. How much do you think is the standard amount taken? Can you also give a sense of how confident you are about your estimate?
Before I tell you the answer, how did you estimate? Did you use a benchmark? What was it?
While you are considering your answer, here is a fascinating chart of blood donation possible matchings according to blood type. Which blood type would you rather be and why?
Source: Wikipedia
The standard NHS blood donation amount is 470ml. Can you picture it? When we discussed this amount it seemed very common to benchmark to a ‘pint’ (which is a very good estimate for the answer), made even more complex because one of us was from the US, where a pint is a completely different measure! It seems bizarre and particularly unhelpful that we can use the same measuring word to mean a substantially different amount across cultural/national boundaries. In fact, within one country alone (Australia) two different quantities with the name ‘pint’ are used! Can you think of any other measures where this kind of ambiguity happens?
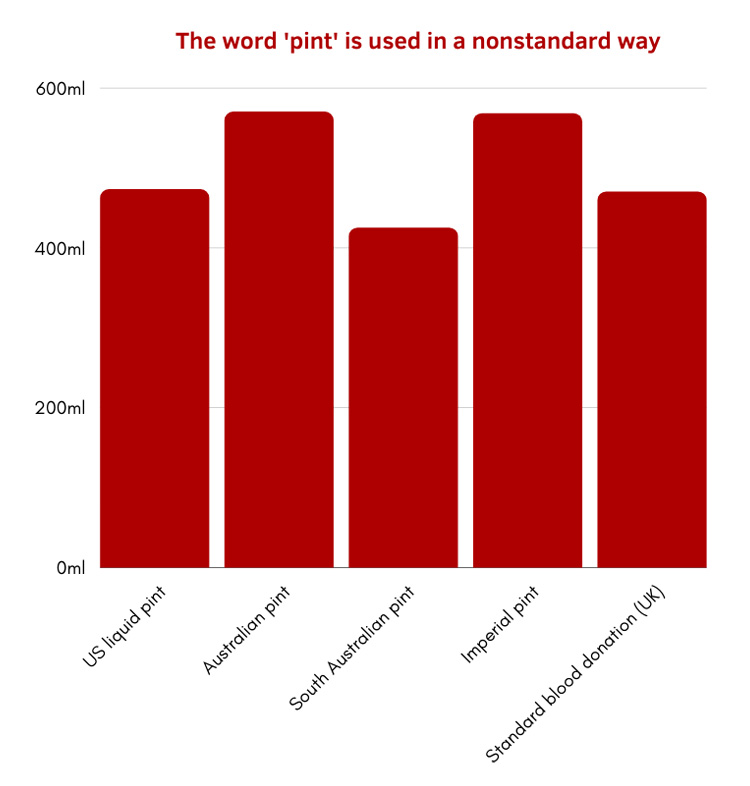
Why did we use a pint as a benchmark for blood? Well, several of us had been in medical situations where we had been informed about blood loss in pints – presumably because it is a good and common measure for people to understand as a benchmark in this way. It is likely also due to the fact that it is not too large and not too small as a proportion of the whole – most people’s bodies contain around 10 (imperial) pints of blood1, and it makes sense that trying to limit benchmark measures to allow them (approximately) to refer to whole numbers between 1 and 20 is likely to make them easier to understand, even if it does result in a trade-off with accuracy. A benchmark is a mental handhold for measure; a pint fits this description nicely because not only is it neatly human-sized (in the sense that it is a glassful that fits in a single hand), but also because we usually have lots of experience with it, in this case perhaps with milk or beer. Of course, that is dangerous to assume – only those over a certain age and within a certain demographic are likely to have experience with either, and in fact my fridge has only contained one litre cartons of almond milk for many years.
It is also interesting to note here how the transfer from the domain of ‘things humans drink that taste nice’ to ‘human bodily fluids’ doesn’t seem to cause too much of an issue or touch on people’s disgust mechanisms. Compare, for example, to measuring something like nasal discharge (snot); benchmarking that using ‘a teaspoon’ or even ‘a (somewhat drippy) forkful’ might feel more inconsistently disgusting to us (unless you are a vampire or a vegan, one of which clubs I do belong to).
Estimation is an interesting mathematical idea because it is both dependent on general skills and specific knowledge. For example, when estimating blood donation volume, general skills might include what we call ‘common sense’, sense of proportion, visualising volumes, multiplicative reasoning, and quantitative reasoning including the ability to make comparisons; specific knowledge might include volume/capacity benchmarks, biological information (like how much blood is in the average human body), and experience of giving blood or seeing someone else do so. Some of both are likely needed; there may be a relationship between the two where more of one can make up for less of the other, but only up to a point. Siegler and Booth suggest that estimating skills “require prior knowledge of the entities whose properties are being estimated” (p.428);2 Poulter and Haylock also add a third dimension, that “performance in estimating is invariably confounded with students' computational ability” (p.28).3
Confidently and flexibly manipulating numbers is also key to estimation. For example, using the knowledge that a blood bag is just over hand-sized and that a can of Coke is about 2/3 of the height of one – and contains around 330ml of liquid – will only get us so far if we are unable to use this information to find and ‘add on’ 1/3 of 330ml correctly, or do the calculation competently in another way. This is another reason why benchmarking in small integer units makes estimation easier and may go some way towards explaining why non-metric measures – confusing as they can be – have stuck around for so long.
References:
- While discussing this, a colleague mentioned that pregnancy increases the amount of blood in the body by around half, which is, surprisingly, true! It can actually vary between 20% and 100% of pre-pregnancy levels by volume, with an average of 45%; see this paper for more detail
- Siegler, R. S., & Booth, J. L. (2004). Development of numerical estimation in young children. Child Development, 75(2), 428–444.
- Poulter, J. G., & Haylock, D. W. (1988). Teaching computational estimation. Mathematics in School, 17(2), 27–29.
Join the conversation: You can tweet us @CambridgeMaths or comment below.