QUESTION 2: comparing approaches to frameworks
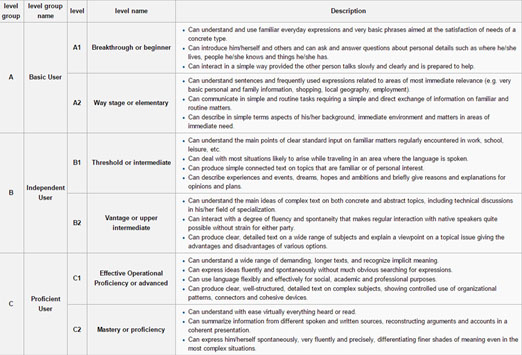
Lynne McClure explains: "I’ve been having conversations and reading up about frameworks, and am intrigued by the similarities and differences between a framework for maths and a framework for languages. There is already a Framework for Mathematics and Numeracy, Netherlands and the well-known Common European Framework of Reference (CEFR) on which it is based. Both of these have general and summative statements for progression and I wonder if this would be a useful starting point and whether it focuses too soon on assessment. The framework for Mathematics and Numeracy focuses on the characteristics of performance tasks, whereas CEFR is in terms of ‘Can do’ statements. Two very different approaches. I attach the statements below.
So my questions are:
1) Would it be useful to give some kind of general and short description for 'performance' at each of the six stages of the Cambridge Mathematics Framework?
2) How would you describe the 'performance' of a beginning mathematician and the progression to the later stages?
3) What words would you use to describe someone who is, for example, very successful at UK Further Maths and understands the landscape and its connections as well as the detail?"
View comments ▼
Statements for progression
The Framework for Mathematics and Numeracy works with six levels of competency:
Z
Z2 - The situation is complex and may require active influencing by adjusting and developing new mathematical models, defining new formulas and adjusting or constructing procedures. More complex computations are required to solve a problem.
Z1 - The situation is complex and may require active influencing by re-modeling mathematical models, redefining formulas and revisiting procedures. More complex computations are required to solve a problem.
Y
Y2 - The situation can be more or less familiar, more complex and requires certain actions based on familiar and set procedures, using known mathematical models, formulas and calculations. More actions are required to solve the problem.
Y1 - The situation can be more or less familiar, more complex and requires certain actions based on familiar and set procedures. More actions are required to solve the problem.
X
X2 - The situation is more or less familiar and unambiguous and clear. Actions are simple and concrete
X1 - The situation is familiar, unambiguous and clear. Actions are simple and concrete.
Common European Framework of Reference (CEFR):